Rabi Oscillation in the Dissociation of H+2
Relevant topics: Molecular Dynamics, Rabi Oscillation, Ultrafast Laser
In light matter interaction, Rabi oscillation is a very common phenomenon. When a two-level system is driven by a laser field, there will be Rabi oscillation. The population will evolve in a sinusoidal manner with the so called Rabi frequency. This is an effective way to control the dynamics in quantum system.
We also find Rabi oscillation in the dissociation of H+2. By controlling the Rabi oscillation, we can control the dissociation rate of H+2. In simulation, we assume that the H+2 is created at the beginning by ionizing an electron from H2. After that, the molecule starts to dissociate. After some time, the nuclear distance reaches a certain value where the \(1s\sigma_g-2p\pi_u\) electronic transition is in resonance with 800nm laser. Then we apply an 800nm fs-laser pulse with defined intensity and profile. Because the motion of neuclei is much slower than the laser pulse, at this point the system can be viewed as a two-level system. In this case, the Rabi frequency depends on the laser intensity and transition dipole. The pulse area determines the final population on state \(1s\sigma_g\) and \(2p\pi_u\). \(2p\pi_u\) will lead to dissociation of the molecule while \(1s\sigma_g\) will not. Thus, the dissociation of H+2 can be controlled by the laser pulse.
However, the effective laser intensity depends on the orientation of the molecule, thus leading to angular-dependent dissociation rate. In simulation, we see node structure in the momentum distribution of proton, as shown in Fig. 1.
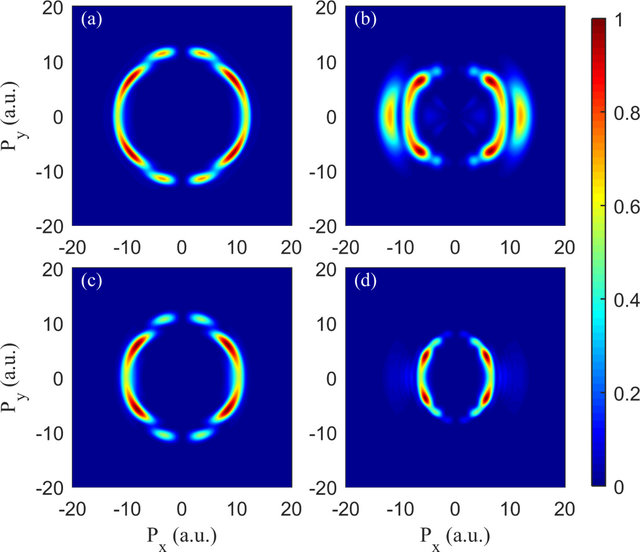
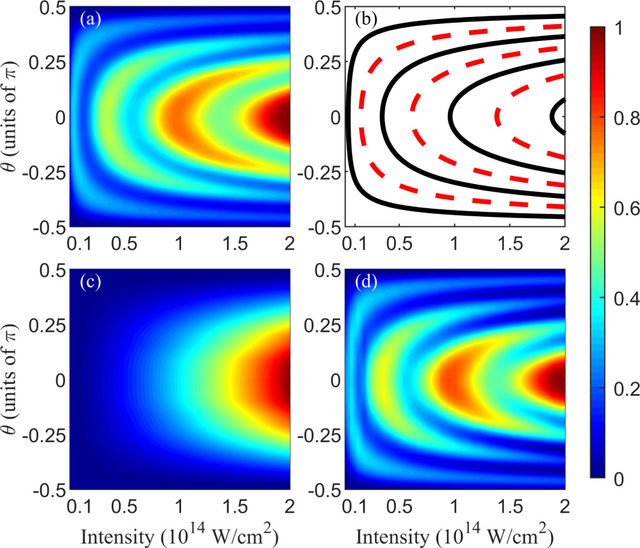
This process is sensitive to intensity, in which focal volume averaging effect plays an important role. If this effect is considered, the node structure in Fig. 1 will be smeared out, leading to a \(\cos^2\theta\)-like structure. To clearly see that, we look at the angular dependent proton momentum distribution with different intensities in Fig. 2. Fig. 2(a) is calculated while assuming the laser intensity is homogeneous. After consiering the focal volume averaging effect, the peak structure is smeared out (shown in Fig. 2(c)). This could explain why the node structure cannot be observed in experiment. Furthermore, we use our matrix-inverse algorithm to retrieve the node structure, as shown in Fig. 2(d).
In this research, we explained the dissociation dynamics of H+2 molecule with a simple Rabi model. We also explained why this effect has not been observed in experiment. Based on this, further control of the dissociation of molecule can be achieved.
This project is supervised by Prof. Feng He in Shanghai Jiao Tong University and mainly contributed by Chenxi Hu. I contributed the part about focal volume averaging effect.
Reference:
- Chen-Xi Hu, Wei-Zhe Li, Wen-Bin Zhang, Xiao-Chun Gong, Jian Wu, and Feng He. "Angle-resolved Rabi flopping in strong-field dissociation of molecules." Physical Review A 103.4 (2021): 043122.