Weizhe Li
Weizhe Li

Focal Volume Averaging Effect

Relevant topics: Strong Field, Ultrafast Laser, Intensity Distribution

Laser is a very useful tool to investigate different systems, including atoms, molecules and solid materials. With the development of ultra-short (~as, 10-18s), ultra-strong (~PW/cm2, 10 15W/cm2) laser pulse, measuring the motion of electrons and nuclei in time domain becomes possible.

The laser intensity can be so high that the electric force acting on the electron is even larger than the Coloumb force from the neuclei. In this case, the processes are very sensitive to laser intensity. Sometimes different models are used for different intensities. However, in experiment, pure laser intensity is not available. The laser pulse always has an intensity distribution. The contributions from different intensiy components are indistinguishable, so the experimental result is always a mixture of them. This is clearly illustrated in Fig.1. Such an effect is called Focal Volume Averaging Effect.

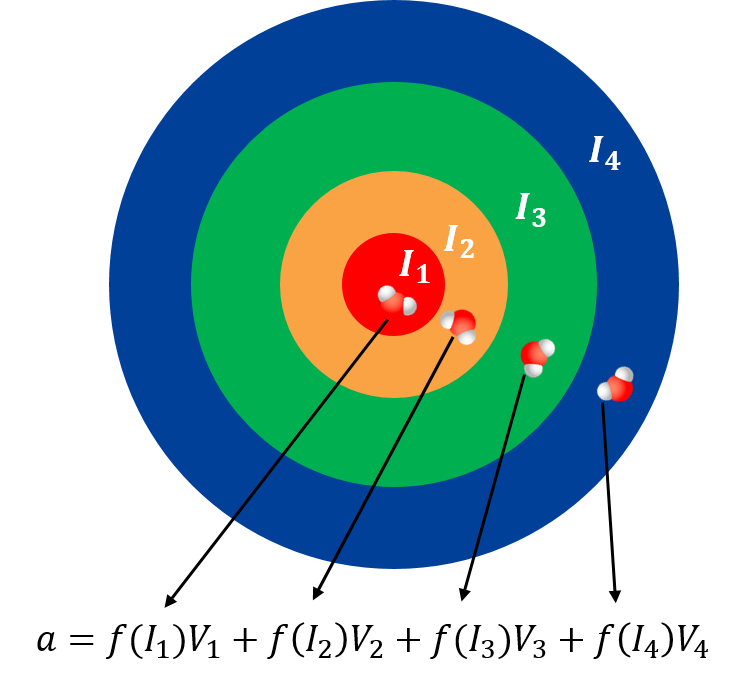
Fig.1. Molecules in the laser focus experience different laser intensities, thus response differently.

For a laser pulse with known intensity distribution, such an averaging effect can be described by linear algebra. If the contribution from different intensities is represented by a column vector and the volumes corresponding to these intensities are written as a row vector, then the result after averging is just the inner product of these two vectors. The row vector can be changed by changing the intensity distribution, for example changing the peak intensity. If we have enough different intensity distributions, then the row vector becomes a matrix, of which the inverse or pseudo inverse can be calculated. Mathematically, the matrix looks like the following [1]:

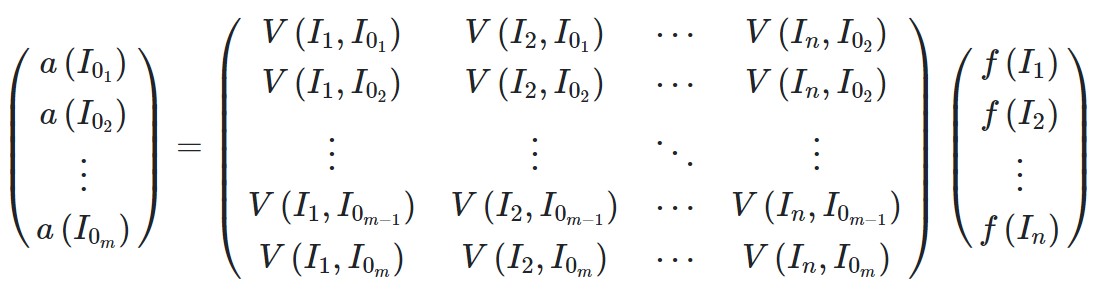
\[ \left(\begin{array}{c}a\left(I_{0_{1}}\right) \\ a\left(I_{0_{2}}\right) \\ \vdots \\ a\left(I_{0_{m}}\right) \end{array}\right)=\left(\begin{array}{ccccc} V\left(I_{1}, I_{0_{1}}\right) & V\left(I_{2}, I_{0_{1}}\right) & \cdots & V\left(I_{n}, I_{0_{2}}\right) \\ V\left(I_{1}, I_{0_{2}}\right) & V\left(I_{2}, I_{0_{2}}\right) & \cdots & V\left(I_{n}, I_{0_{2}}\right) \\ \vdots & \vdots & \ddots & \vdots \\ V\left(I_{1}, I_{0_{m-1}}\right) & V\left(I_{2}, I_{0_{m-1}}\right) & \cdots & V\left(I_{n}, I_{0_{m-1}}\right) \\ V\left(I_{1}, I_{0_{m}}\right) & V\left(I_{2}, I_{0_{m}}\right) & \cdots & V\left(I_{n}, I_{0_{m}}\right) \end{array}\right)\left(\begin{array}{c} f\left(I_{1}\right) \\ f\left(I_{2}\right) \\ \vdots \\ f\left(I_{n}\right) \end{array}\right) \]
Thus, the focal volume averaging effect can be eliminated numerically. The method has been proved valid in simulation.

This research project was supervised by Prof. Feng He in Shanghai Jiao Tong University

Reference:
  1. Chen-Xi Hu, Wei-Zhe Li, Wen-Bin Zhang, Xiao-Chun Gong, Jian Wu, and Feng He. "Angle-resolved Rabi flopping in strong-field dissociation of molecules." Physical Review A 103.4 (2021): 043122.